6.1. Смешение в объёме


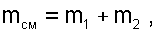
Смешение в объёме – это смешение веществ (газов, паров, жидкостей) за счёт их взаимного диффузионного проникновения после удаления (разрушения) разделяющих их непроницаемых перегородок и без изменения суммарного объёма веществ.

Допустим, что в двух отсеках сосуда (рис. 6.1) объёмом V, разделённого адиабатной перегородкой, находятся разные газы при разных давлениях и температурах.

Перегородка разрушается и происходит диффузионное смешение газов. При этом масса смеси оказывается равной сумме масс смешивающихся газов

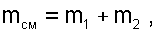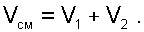а объём – сумме первоначальных объёмов этих газов


В результате удельный объём смеси двух или более компонентов газов будет, определятся как:

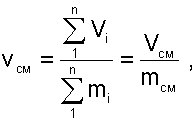(6.1)


где n – число смешивающихся компонентов газа.

Для определения параметров состояния смеси газов, с известным массовым составом и известными параметрами газов до смешения, необходимо знать ещё один параметр. Он определяется на основании первого закона термодинамики для данной системы


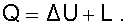При адиабатном смешении газов без изменения общего объёма сосуда, теплота и работа изменения объема равны нулю (Q=0, L=0). Следовательно, изменения внутренней энергии в системе нет, т.е. внутренняя энергия после смешения равна сумме внутренних энергий компонентов смеси до смешения:

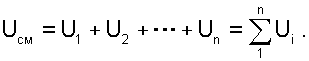(6.2)


Используя аддитивные свойства (подчинение закону суммирования) внутренней энергии, после деления выражения (6.2) на массу смеси, получаем расчётное выражение удельной внутренней энергии газа после смешения:

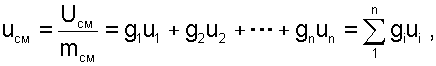(6.3)


где gi=mi/mСМ – массовые доли компонентов смеси газов.

Удельный объём (vСМ) и удельная внутренняя энергия (uСМ) при известном составе смеси, определяет состояние смеси. По ним могут быть найдены остальные параметры смеси. Для реальных газов они обычно определяются по таблицам термодинамических свойств веществ.

Для идеальных газов внутренняя энергия функция только температуры, и поэтому задача определения параметров смеси упрощается. Приняв начало отсчёта внутренней энергии при 0 ОC и, считая постоянной изохорную теплоемкость идеальных газов, можно записать:

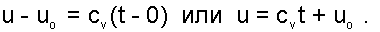(6.4)


Используя выражение (6.4) для определения всех внутренних энергий газов, получим выражение (6.3) для смеси идеальных газов в виде:

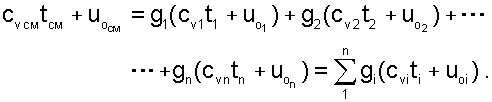(6.5)


где cVi – массовые изохорные теплоёмкости компонентов смеси газов;
ti - температура компонентов смеси газов до начала процесса смешения, ОC;
uОi – удельная внутренняя энергия компонентов смеси газов до начала процесса смешения при 0 ОC.

По закону сложения (аддитивности) внутренняя энергия смеси газов при 0 ОC будет равна сумме внутренних энергий ее компонентов при той же температуре:

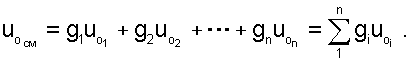(6.6)


Следовательно выражение (6.5) примет вид:

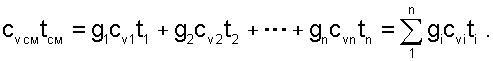(6.7)


Выразив теплоёмкость смеси газов через сумму теплоемкостей ее компонентов


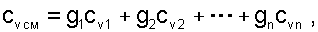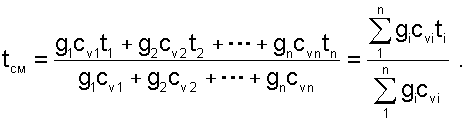получим из уравнения (6.7) расчётное выражение для температуры смеси идеальных газов:

(6.8)


Выражение (6.8) справедливо и при подстановке всех температур по абсолютной шкале Кельвина.

Далее, зная vСМ и TСМ для идеальных газов можно определить давление смеси, используя уравнение состояния идеального газа:


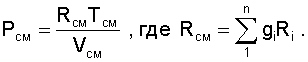Изменение энтропии системы в расчёте на один килограмм смеси определяется как сумма изменений энтропий компонентов смеси газа:

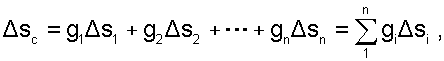(6.9)


где Dsi = siСМ - si – изменение энтропии одного компонента смеси газа от начальных параметров до параметров смеси. Выражение (6.9) справедливо для реальных и идеальных газов.

Для идеальных газов Dsi рассчитывается по формулам идеальных газов, через любую пару параметров. При этом необходимо использовать параметры парциального давления каждого компонента смеси газа. Например, для первого компонента можно записать:

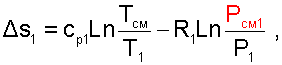(6.10)


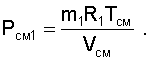где – РСМ1 парциальное давление первого компонента смеси газа при температуре смеси, когда этот газ занимает весь объем и соответствует выражению

Потери потенциальновозможной полезной работы газа (эксергии) в этом необратимом процессе ведутся традиционно по теореме Гюи-Стодолы [1]:


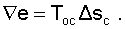Используя выражения 6.1-6.8 можно решить и обратную задачу – нахождения масс или массовых долей компонентов смеси данных газов при известных их начальных параметрах, необходимых для получения необходимых параметров смеси газов.

предыдущий параграф содержание следующий параграф