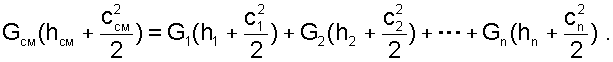
(6.11)
Смешение в потоке – это слияние нескольких потоков веществ в общий поток.
Давление вещества в месте смешения должно быть ниже минимального или равно минимальному давлению смешивающихся потоков, т.е. в расчетах оно должно быть задано.
Рассмотрим пример адиабатного смешения потоков в трубопроводах (рис. 6.2). Обозначим расходы смешивающихся потоков как G1, G2,..., Gn.
Предположим, что известны массовые расходы потоков, параметры смешивающихся потоков и давление смеси. Воспользуемся для этого процесса смешения уравнением первого закона термодинамики для потока, при отсутствии теплообмена системы с внешней средой (q=0) и технической работы (lТ=0):
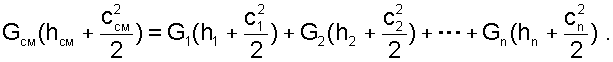 |
(6.11) |
В технических устройствах кинетическая энергия потоков, а соответственно и её изменение в процессе смешения очень малы по отношению к энтальпиям смешивающихся веществ, поэтому обычно условно принимают, что c1=c2=...=cn=cСМ, а так как GСМ=G1+G2+...+Gn, то уравнение первого закона термодинамики для потока будет иметь вид:
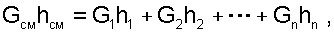 |
(6.12) |
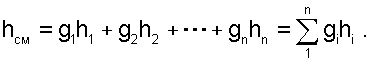 |
(6.13) |
Давление РСМ и энтальпия hСМ определяют состояние смеси вещества заданного состава. Определение других параметров смеси реальных веществ ведётся по таблицам термодинамических свойств отдельных компонентов. Проще выполняется определение параметров смеси потоков веществ с одинаковыми физическими свойствами (например, воды и водяного пара). В этом случае используются таблицы термодинамических свойств данного вещества.
Ещё проще по РСМ и hСМ определяются все остальные параметры смеси идеальных газов. Для идеальных газов, приняв начало отсчета энтальпии от 0 ОС и используя ее постоянные изобарные теплоемкости, уравнение (6.13) можно представить в виде:
 |
(6.14) |
Все преобразования энтальпий идеальных газов в уравнении (6.14) аналогичны преобразованиям внутренних энергий для случая смешения в объёме. Температура смеси, выраженная из (6.14), определяется как:
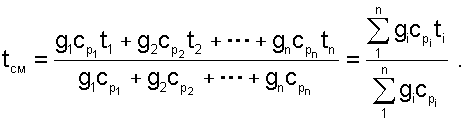 |
(6.15) |
Выражение 6.15 справедливо и при подстановке в него всех температур по абсолютной шкале Кельвина.
По РСМ и tСМ для идеальных газов могут быть определены все другие параметры смеси, например:
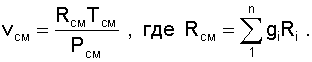 |
Необратимость процесса смешения в потоке оценивается по увеличению энтропии системы, аналогично смешению в объёме по формуле (6.9). Для идеального газа, изменение энтропии каждого потока смешения определяется по температуре и давлению до смешения, и по температуре смеси и парциальному давлению этого компонента смеси (6.10). Например, для первого потока:
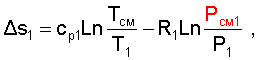 |
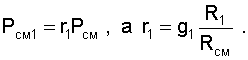 |
Потеря эксергии при смешении в потоке определяется, как во всех случаях, по формуле Гюи-Стодолы [1].
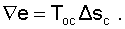 |
Изменение параметров при смешении в потоке и необратимость этого процесса можно наглядно показать в h,s- диаграмме. Наиболее просто это можно сделать для процессов смешения потоков одного и того же вещества с разными начальными состояниями. Такие процессы широко используются в технике, например: смешиваются в общем паропроводе два потока пара; вспрыски воды в паропроводы для регулирования перегрева пара; смешение в эжекторах, струйных насосах и т.д..
Рассмотрим смешение двух потоков одного и того же газа с одинаковыми давлениями до и после смешения и различными начальными температурами, определяемыми точками 1 и 2 в диаграмме h,s (рис. 6.3).
В соответствии с формулой (6.13) для двухкомпонентной смеси ее энтальпия определяется как:
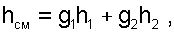 |
(6.16) |
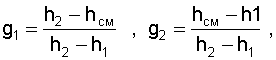 |
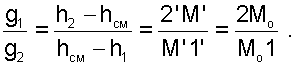 |
(6.17) |
Таким образом, графическое определение энтальпии смеси сводится к делению отрезка прямой 2'1' – точка М' или 12 – точка МО пропорционально массовым долям смешивающихся потоков. Аналогично энтальпии смеси в точке MО, энтропии этой точки соответствует значение:
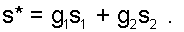 |
(6.18) |
Действительная энтропия смешивающихся потоков находится правее точки MО на пересечении линии постоянной энтальпии hСМ и изобары смеси, что соответствует точке M. Процесс смешения необратим и характеризуется увеличением энтропии системы на величину:
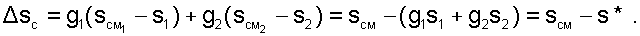 |
(6.19) |
Прямая 12 называется прямой обратимого смешения. Она позволяет графически показать увеличение энтропии системы в процессах смешения потоков.
Приведём некоторые типичные процессы смешения потоков и их графическое представление в h,s- диаграммах.
На рис. 6.3 показан процесс смешения двух потоков одного газа с одинаковыми давлениями и разными температурами. До смешения состояние газов соответствовало точкам 1 и 2 , после смешения – точке M. Все точки лежат на одной изобаре. Проведя, прямую 12, на пересечении её с hСМ найдём точку MО. Разница энтропий точек M и MО соответствует увеличению энтропии системы в данном процессе смешения потоков газа.
Рис. 6.4. Графическое изображение в h,s- диаграмме увеличения энтропии системы при смешении двух одинаковых веществ с давлениями Р2>P1=PСМ
На рис. 6.4 представлен процесс смешения двух потоков одного газа при разных давлениях и температурах.
При этом давление смеси равно меньшему давлению одного из потоков, т.е. Р2>P1=PСМ. Возрастание энтропии за счёт необратимости процесса смешения в этом случае вызывается не только необратимостью теплообмена между потоками, но и дросселированием второго потока до давления первого.
На рис. 6.5 представлен процесс смешения двух потоков одного газа при разных давлениях и температурах. При этом давление смеси меньше давления меньшего из смешивающихся потоков, т.е. Р2>P1>PСМ.
На практике возможно частичное использование располагаемой работы потока высокого давления для повышения давления потока с низким давлением в специальных устройствах смешения – эжекторах. На рис. 6.6 и приведена схема такой установки, а на рис. 6.7 изображён идеальный процесс смешения потоков одинаковых веществ в эжекторе.
Для пояснения этого процесса, его можно условно разбить на три составляющие: адиабатное необратимое дросселирование первого потока через кольцевой зазор В до давления в камере смешения (процесс 11’) и процесс необратимого адиабатного истечения газа через сопло А второго потока (процесс 22’), оба эти процесса идут до давления Pmin в камере смешения С, которое ниже давления смеси и давления Р1. Далее идёт процесс смешения этих потоков при постоянном давлении Pmin до состояния, соответствующего точке 3, после чего в диффузорной части эжектора D идёт процесс необратимого адиабатного торможения потока до давления РСМ, (процесс 3M). Увеличение энтропии системы в этом случае определяется также с помощью прямой 12 в виде отрезка прямой МОМ.
Основные потери эжектора обусловлены необратимостью перемешивания в камере смешения двух потоков с разными параметрами и разными скоростями.
| предыдущий параграф | содержание | следующий параграф |